t = {C × (V0 - V1)} / I
t = 0.5 × C × (V02 - V12) / P
t = -C × R × ln (V1 / V0)
Ah = 0.5 × C × V02 / (3600 × Vb)
| t | Discharge time (sec.) |
| C | Capacitance (F) |
| V0 | Charge voltage (V) |
| V1 | Discharge voltage (V) |
| Vb | Nominal battery voltage (V) |
| I | Discharge current (A) |
| R | Discharge resistance (Ω) |
| P | power (W) |
C = I × t / (V0 - V1)
C = 2 × P × t / (V02 - V12)
C = -t / {R × ln (V1 / V0)}
In the case of large current discharge, it needs to consider the IR drop, which is caused during the early discharge stage derived from capacitor's IR (direct current resistance) and the discharge current.
In the case of small current discharge, it needs to consider the discharge current of the capacitor (self-discharge).
The motion back up, such as RAM and RTC is generally constant current.
As an example, charging DB series 5.5V 1F with 5V and discharge until 3V with 1mA of constant current.
The discharging time would be that charging voltage of V0 is 5.0V, the voltage V1 becomes 3.0V after discharge. Also since the discharge current I is 1mA, it would be 0.001A.
From Calculation ①, discharge time t = {C x (V0 - V1)} / I = {1F x (5.0V - 3.0V)} / 0.001A = 2000 seconds. Therefore it would calculate 33 minutes of backup.
As another example - calculating the necessary capacitance for 1-hour back up with RTC, which works with 2.0V to 1.0V of motion voltage range and 10µA of used current.
From Calculation ①, the capacitance would be: C = I x t / (V0 - V1). From the conditions, it would be:
C = (10 x 10-6A) x 3600s / (2.0V - 1.0V) = 0.036F
Therefore, it would be able to work with 3.3V0.2 F（Size φ6.8x1.4mm) from DSK series.
However, it needs to consider the decrease rate of voltage from the self discharge in the case of micro-current. It is recommend to check the working duration with RTC and the capacitors.
In general, it is common to use constant power for discharge in the conditions, such as driving motors, lighten LED by DC-DC converter with maintained output voltage, etc.
As an example, by using DZ series 2.5V 100F, calculating the operation time for turning on LED with 5V 10mA consecutively for the rage of 2.5V to 1.0V with DC-DC converter to increase to 5V.
The power needed for LED would be 5V x 10mA = 0.05W.
From the calculation ②, t = 0.5 x C x (V02 - V12) / P = 0.5 x 100F x (2.5V2 - 1.0V2) / 0.05W = 5250 seconds, which means about 87 minutes. It would allow consecutively turning on for about 87 minutes. In reality, it is necessary to calculate the converting rate of DC-DC converter; therefore, it would be 70 minutes with 80% of the efficiency rate.
Then it is expected to have 3500 minutes (about 58 hours) since it operates only for 20m sec. per 1 second.
As another example - calculating the required capacitance to operate 10 minutes for the range of 2.5V to 1V with 1W.
By using the formula ②, C = 2 x P x t / (V02 - V12). With the requirements, the calculation would be:
C = 2 x 1W x 600s / (2.5V2 - 1.0V2) = 228F
Therefore, by choosing ELNA's DZH series 2.5V 300F (size φ35x50mm), it would allow to operate for around 13 minutes.
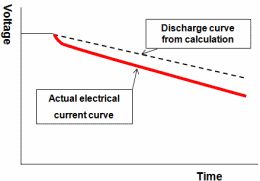
Please confirm the following when there is a difference at actual discharge time and the calculated discharge time.
Measuring DC Resistance and IR Drop
If the discharge current is large, IR drop occurs from the accumulation of DC internal resistance and the electric current.
For the short time, IR drop can be assumed as ΔV1; however, the DC internal resistance is required to be calculated from ΔV2/I by IEC standard
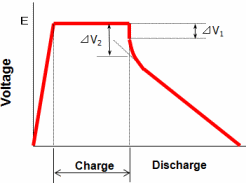
Rd = ΔV2 / I
Effect of Self-discharge
DLC has self-discharge with small electrical current.
Therefore, when DLC needs to operate for long time with small electricity after charging, it is necessary to calculate the discharge time with consideration of self-discharge.
By adding the decrease of voltage derived from the self discharge, the calculation would be closer to the voltage perseverance characteristics data.
Also, the self-discharge depends on the charging time and the ambient temperature.
